Planning & estimating
This chapter delves into essential measurement concepts and conversion techniques that are fundamental to accurate planning and estimating in construction projects, a topic that makes up around 17% of the test. Understanding these principles is crucial for ensuring precise scope of work, identifying potential design or construction errors, and performing field inspections with accuracy. You'll learn to effectively use tools like the architectural scale and basic calculator to convert units and calculate dimensions in linear, square, and cubic measurements. Mastery of these skills will enable you to coordinate projects seamlessly, adhere to code compliance, and develop accurate cost estimates for materials, equipment, and labor, all of which are vital for successful project execution.
Items provided during the exam
For the examination, the following materials will be supplied by the state: an architectural scale, a basic calculator, a dry erase board, and an estimating handout.
Converting inches into feet
For many formulas, it's crucial to use a consistent set of measurement units. On the exam, remember to multiply inches by inches or feet by feet. It's not permissible to multiply feet by inches. To multiply these two measurements, convert inches into feet or vice versa.
A foot has 12 inches. To convert inches into feet, divide the inches by 12 to get the units in decimal feet. For instance, 3 feet 4 inches will be input into the calculator as 3.333.
The below table provides a quick conversion guide from inches to decimal feet. Similarly, to convert feet into inches, multiply the feet by 12.
Inches to Feet Conversion:
- 1 inch
- Fraction feet: 1/12
- Decimal feet: 0.083
- 2 inches
- Fraction feet: 2/12
- Decimal feet: 0.167
- 3 inches
- Fraction feet: 3/12
- Decimal feet: 0.25
- 4 inches
- Fraction feet: 4/12
- Decimal feet: 0.333
- 5 inches
- Fraction feet: 5/12
- Decimal feet: 0.417
- 6 inches
- Fraction feet: 6/12
- Decimal feet: 0.5
- 7 inches
- Fraction feet: 7/12
- Decimal feet: 0.583
- 8 inches
- Fraction feet: 8/12
- Decimal feet: 0.667
- 9 inches
- Fraction feet: 9/12
- Decimal feet: 0.75
- 10 inches
- Fraction feet: 10/12
- Decimal feet: 0.833
- 11 inches
- Fraction feet: 11/12
- Decimal feet: 0.917
- 12 inches
- Fraction feet: 12/12
- Decimal feet: 1.0
Decimal Conversion Guide
General Conversion Numbers
Below are other useful measurement conversions used in construction.
Linear Measurements:
- 1 foot = 12 inches
- 1 yard = 3 feet
- 1 yard = 36 inches
- 1 mile = 5,280 feet
Area Measurements:
- 1 square foot = 144 square inches
- 1 square yard = 9 square feet
- 1 acre = 43,560 square feet
- 1 square mile = 640 acres
Volume Measurements:
- 1 cubic yard = 27 cubic feet
- 1 cubic yard = 46,656 cubic inches
- 1 cubic foot = 1,728 cubic inches
- 1 cubic foot of water = 7.48052 gallons
Metric Conversions:
- 1 meter = 3.28 feet
- 1 inch = 2.54 centimeters
Other Conversions:
- 1 roofing square = 100 square feet
- 1 cubic yard = 81 square feet at 4 inches deep
Architectural Scale
Architectural Scale 1
The key purpose of an architectural scale or ruler is to accurately measure actual dimensions or lengths on a scaled drawing. This tool is particularly useful when dealing with construction drawings or blueprints that have been scaled down to fit a standard-sized piece of paper, despite representing large structures, areas or objects.
It is crucial to identify the scale of the drawing or object to be measured before using an architectural scale. Once the scale has been determined, you need to select the corresponding scale on the ruler. For instance, a 1/8 marking on the ruler translates a 1/8 inch on the drawing to 1 foot, indicated on the drawing as "1/8" = 1 foot". It's important to exercise caution while choosing the scale on the ruler since each edge has two scales – one that reads from left to right and another that reads from right to left.
When employing the ruler, align the zero marker with the start of the object to be measured and identify the object's endpoint. Use the scale to gauge the item's length. If the length measured isn't a whole number, round it down to the nearest whole number. This value represents the length in whole feet.
The zero end of the ruler showcased in below image features compressed markings, which represent fractional feet. To measure an item's precise length, reposition the scale ruler so that the object's endpoint aligns with the whole feet marking on the ruler.
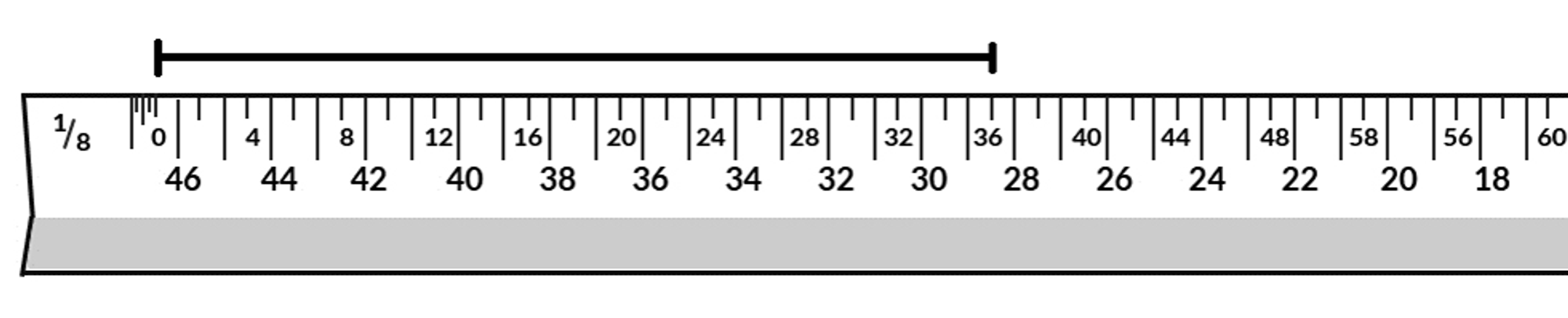
Architectural Scale Example
Consider an example where a line, on a scaled drawing, slightly exceeds 36 feet. Position the zero mark on the scale at the point representing 36 feet. The part of the line extending beyond this point will fall into the section of the scale marked with compressed ticks, each representing a fraction of a foot. If the line extends beyond the zero indicator by six ticks, each tick represents 1/6 of a foot or 2 inches. Once you've counted the ticks, add the equivalent inch measurement to the original measurement in feet.
1 Courtesy of GEI International, Inc. Syracuse NY
Linear Measurements
For measurements of items such as casings, baseboards, and lengths of wire, you'll use linear feet. This simply measures the distance between two points. In the below image, you can see an example of a linear measurement equivalent to 1 foot or 12 inches.

Linear measurement of 1 foot
A real-world application of this concept could be determining the total linear length of baseboard required to border the walls. In order to work out the amount of baseboard necessary, we need to calculate the total linear distance of the walls. This is done by summing up the lengths of each wall.

Square
By adding up 10’ + 10’ + 10’ + 10’, we get a total of 40 linear feet.
So, the room will require 40 linear feet of baseboard.
WARNING: Multiplying 10’x10’ will give you the area of the room, not the linear footage.
Area
To find the area of a rectangle, the width is multiplied by the length. As such, the total square footage of a room, crucial for working out how much hardwood flooring is required, must be ascertained.
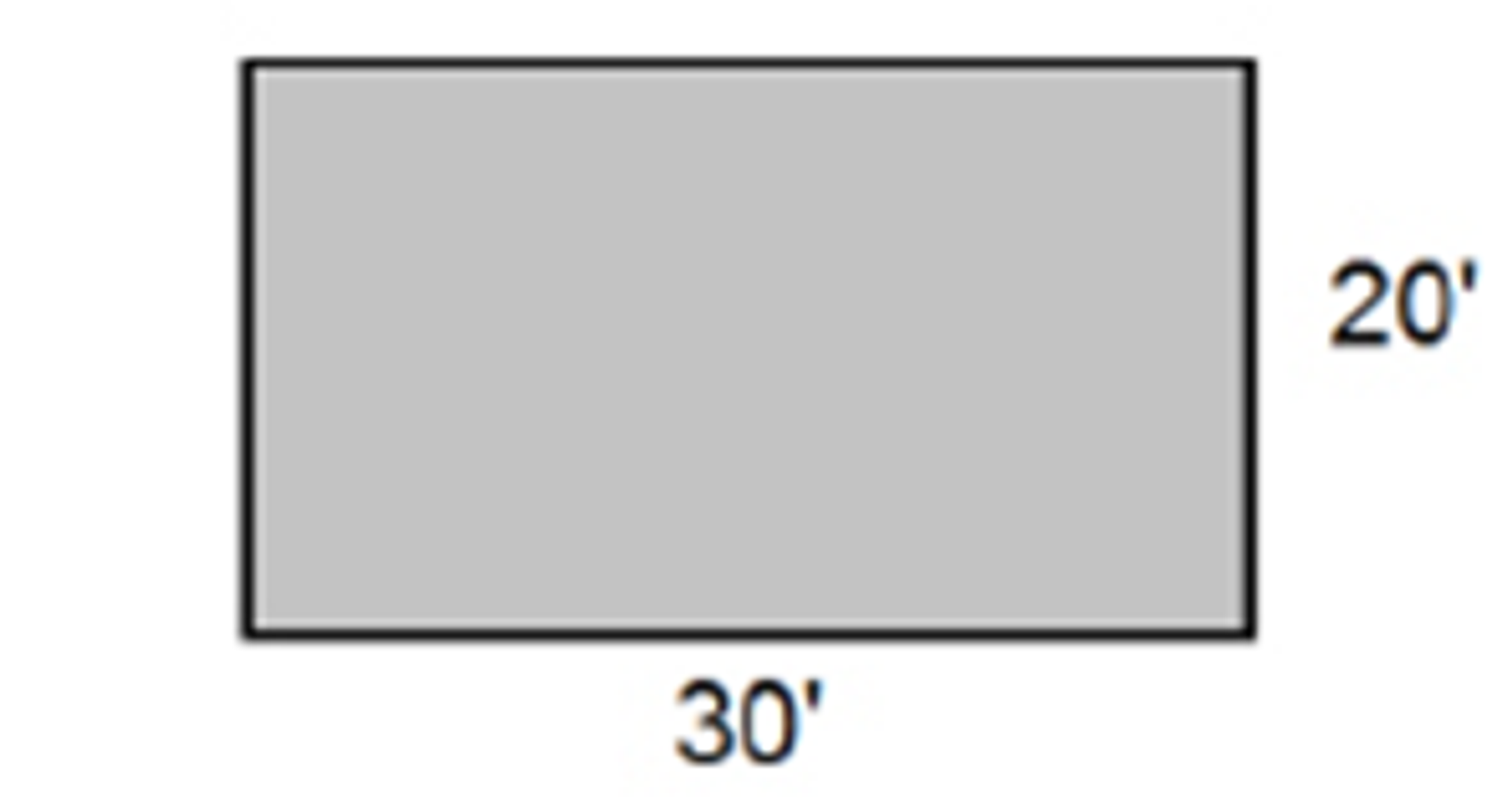
Rectangle Area
Area = Length x Width
Consider a room of size 30’ by 20’ (the above figure). To find the total area, multiply the length by the width.
30’ X 20’ = 600 sq ft (ft2)
As a result, you'll need 600 sq ft of hardwood material to completely cover the room's floor area.
Volume
The volume of a rectangular object can be calculated by multiplying its height, width, and length together. Take concrete for example, which can be measured in either cubic feet or cubic yards, but is typically ordered in cubic yards.

Rectangular volume
Volume = Length x Width x Height
As demonstrated in above figure, a cube has a volume of 6,000 cubic feet (cu ft), calculated by 30 x 10 x 20. Given that concrete is typically quantified and ordered in terms of cubic yards rather than cubic feet, it's necessary to convert cubic feet into cubic yards. This can be achieved by dividing the quantity in cubic feet by 27, as 1 cubic yard equals 27 cubic feet.
6000 ÷ 27 = 222.22 cubic yards
Circle Basics
The circumference of a circle refers to the distance around it. The diameter, as shown in the below figure, is the line that runs straight through the circle's center from one side to the other. The radius, on the other hand, is the line that goes from the circle's center to its perimeter.
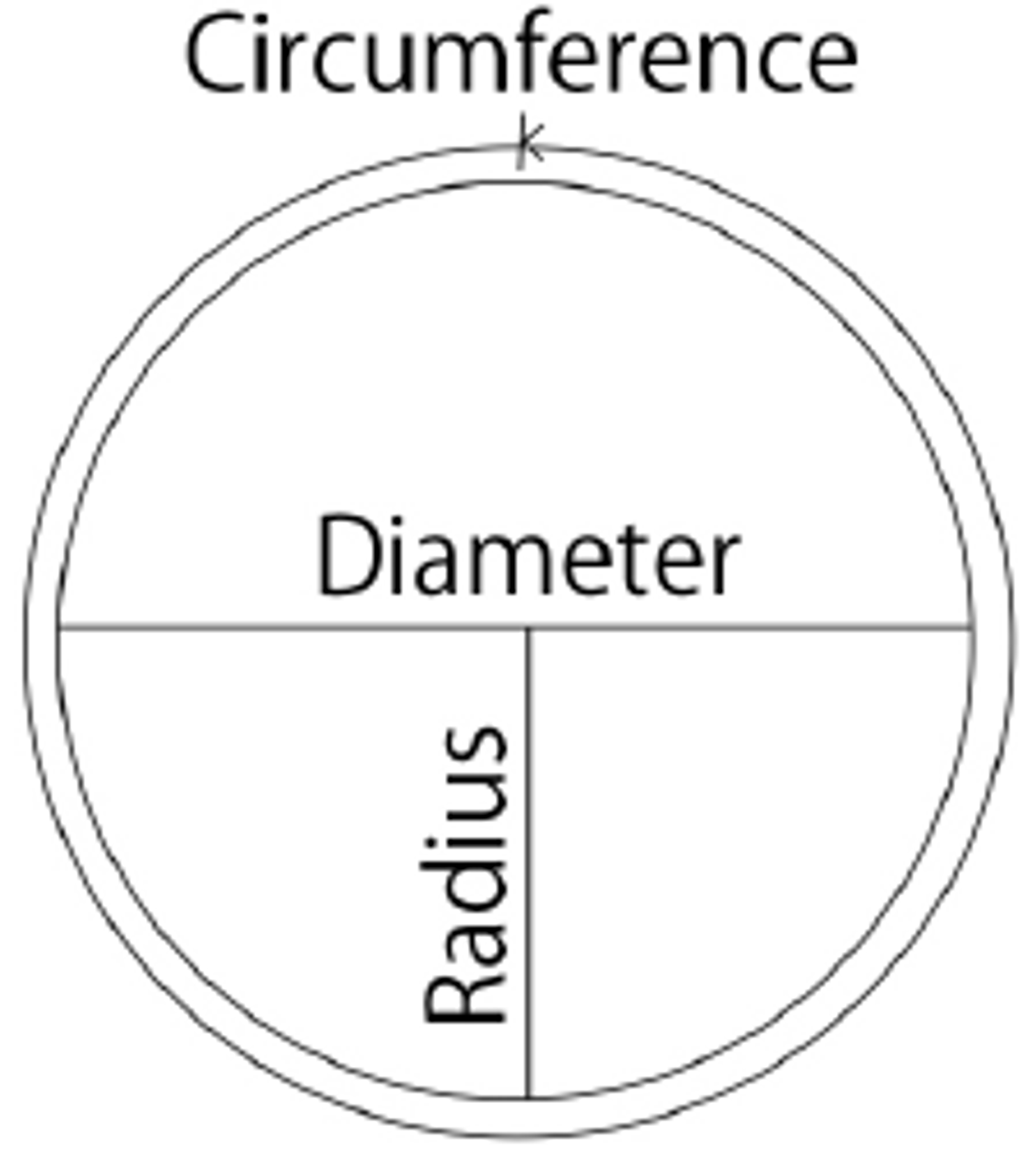
Circle basics
Remember these key points:
- The diameter is equal to twice the radius.
- The radius is always half of the diameter.
- The circumference is 3.14 times the diameter.
Let's consider a circle with a radius of 2 feet:
Diameter = 4 feet (2 feet x 2)
Circumference = 12.56 feet (4 feet x 3.14)
Area of a Circle
There are two methods to compute the area of a circle. One is the conventional formula (π×r2), and the other is a more straightforward approach. The standard formulas can be complex when determining the basic area of a circle. An easier alternative is to imagine the circle as a square. Once the area of the square is known, multiply that area by 78.5% (0.785).
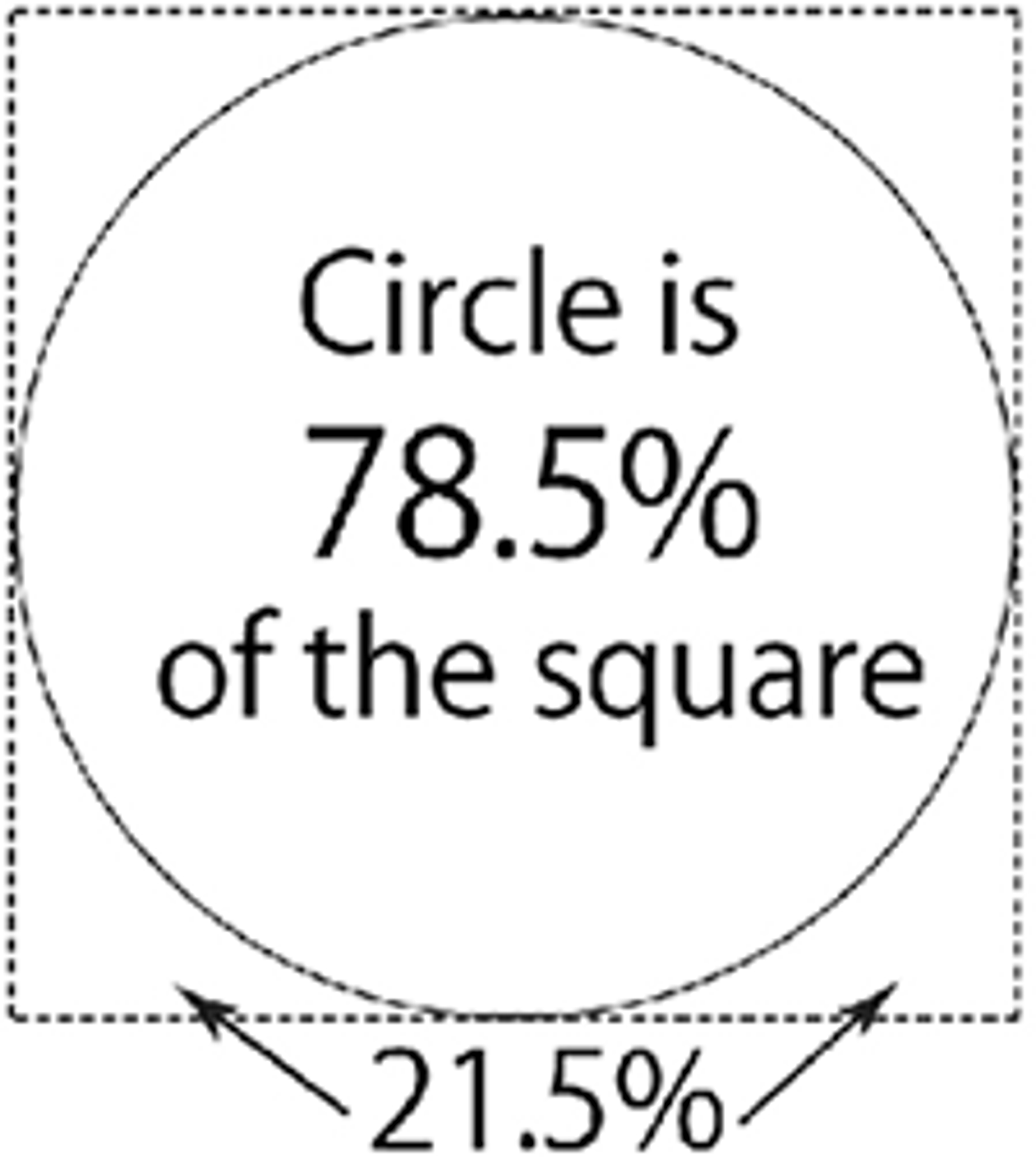
Area of the circle
Envision a circle occupying 78.5% of the total area of a square (above figure), while the remaining 21.5% is taken up by the corners that the circle doesn't cover.
If you have a circle with a diameter of 20 feet, the corresponding square would have an area of 20’ x 20’, or 400 sq ft.
To find the circle’s area, multiply the area of the square (400 sq ft) by 78.5%.
400 sq ft x 0.785 equals 314 sq ft.
Volume of a Cylinder
The calculation of a cylinder's volume is akin to that of a circle, but with the addition of height as the third dimension. Visualize a cylinder occupying 78.5% of the cubic volume of a rectangle.
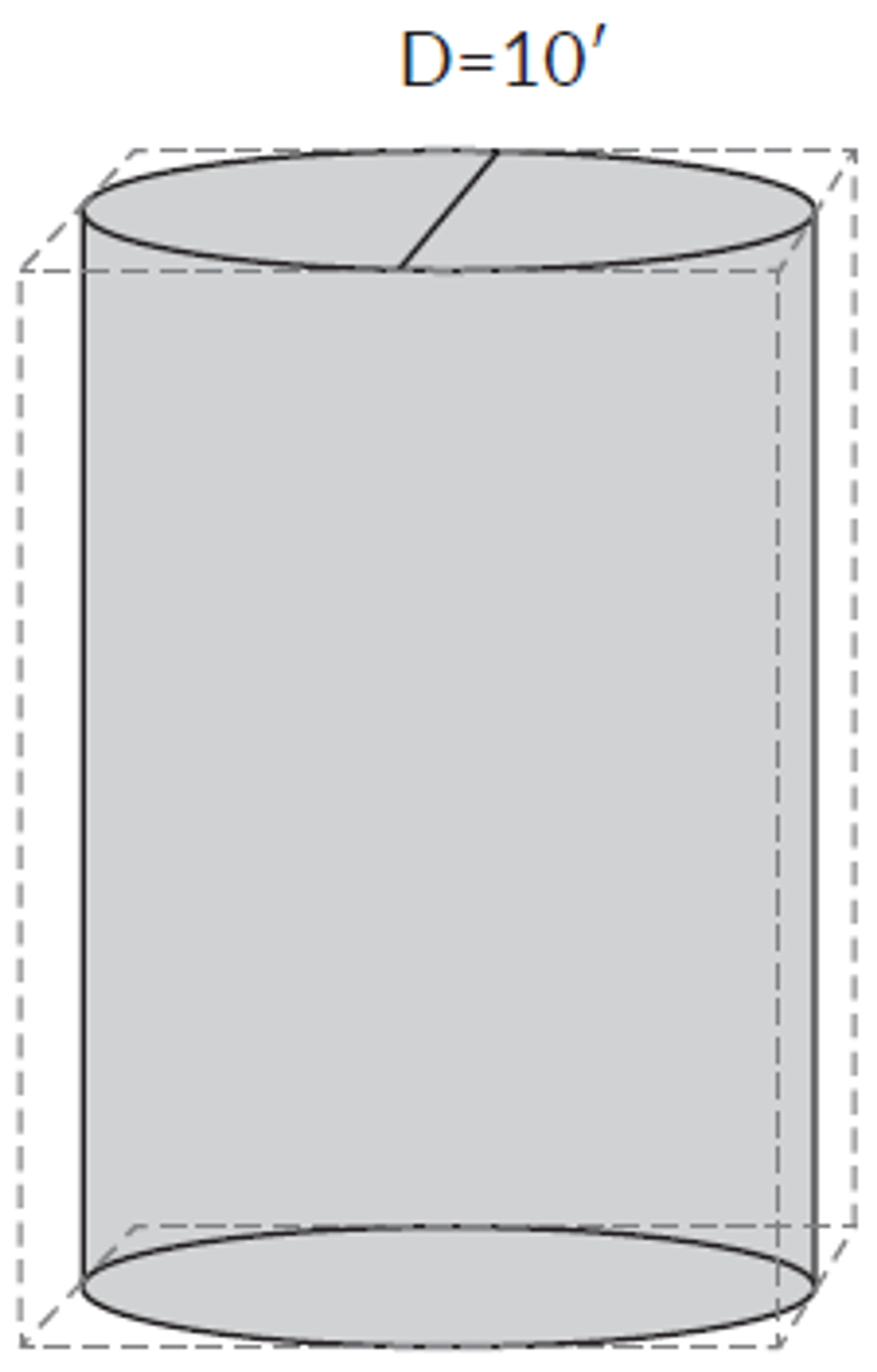
Volume of the cylinder
In the above image, a cylinder is shown with a diameter of 10’ and a height of 20’.
Start by calculating the volume of the equivalent rectangle. As the diameter is 10’, both the length and width will be the same, 10’.
The volume is then 10’ x 10’ x 20’, which equals 2000 cubic feet (cu ft).
To find the volume of the cylinder, multiply the volume of the rectangle, in this case, 2000 cubic feet, by 78.5% (0.785). This equals 1570 cubic feet.
Triangle
The method for finding the area of a triangle is a slightly tweaked version of the one used for rectangles or squares.
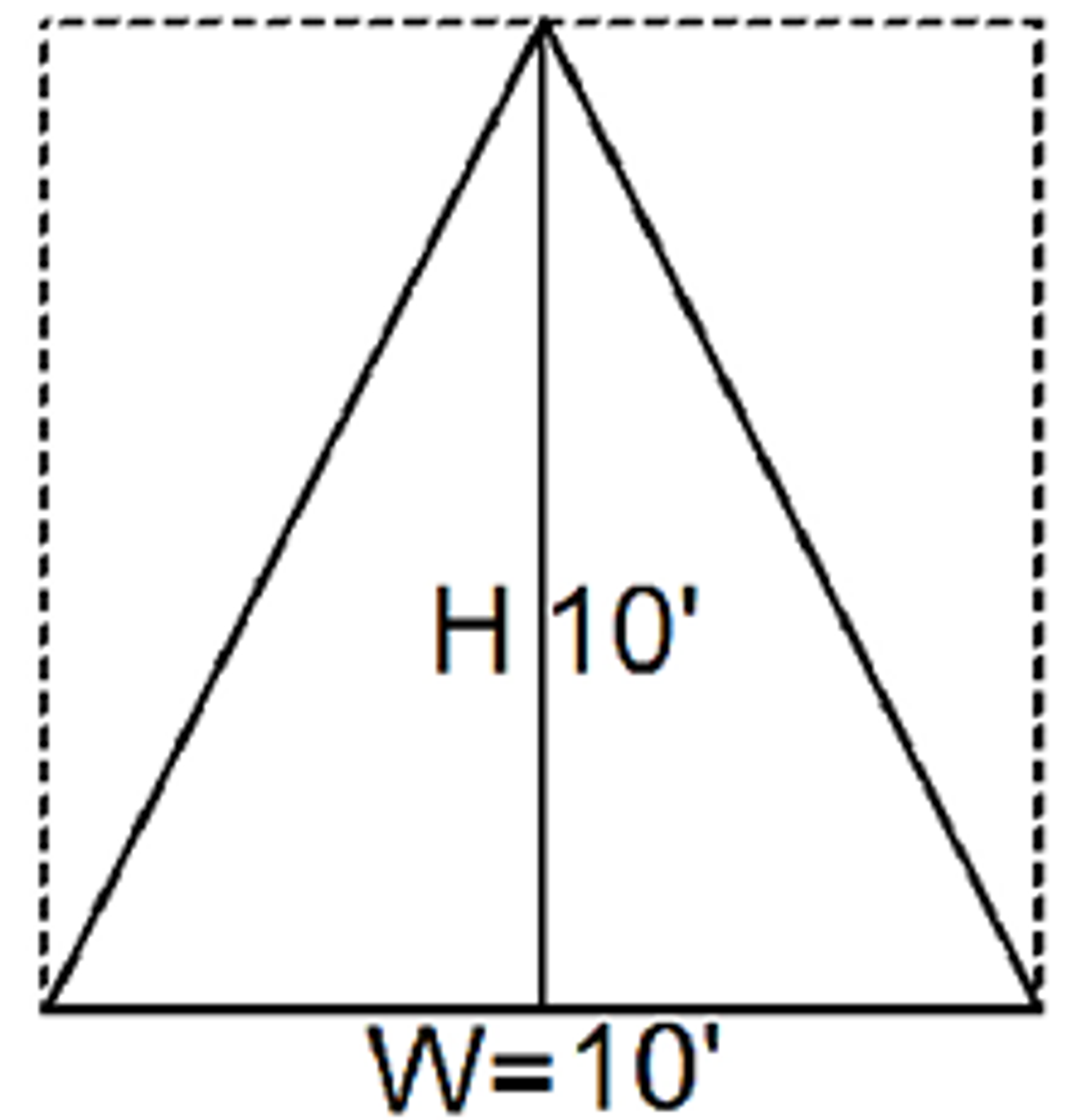
Area of the Triangle
Depicted in the above area is a triangle with dimensions of 10' for both the height and width. To begin, determine the area of a square or rectangle by multiplying the height and width together.
10' x 10' equals 100 sq ft, representing a square or rectangle's area.
Keep in mind, the area of a triangle is half that of a square or rectangle. Hence, divide 100 sq ft by 2 to find the area of the triangle.
100 ÷ 2 = 50 sq ft
Triangle and Rectangle Combination
It's common to encounter scenarios where both a triangle and rectangle's combined area needs to be calculated, such as when assessing a gable roof and wall. While you can break down the shape into a rectangle and triangle and calculate the area separately, you can also use a more straightforward method involving just two calculations.
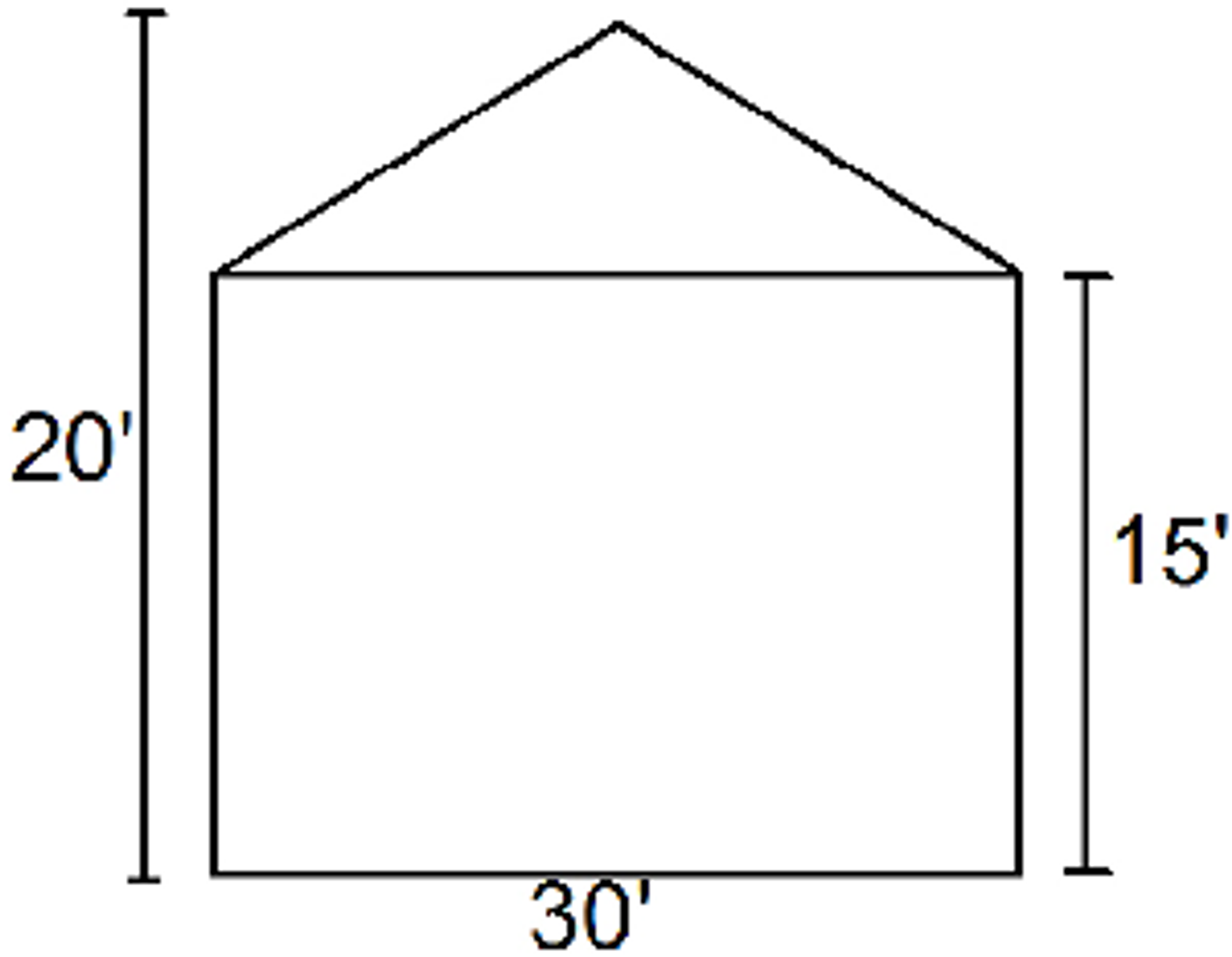
Triangle/rectangle combination
Consider an example depicted in the figure where we have a triangle and a rectangle. The height of the base square is 15’ and the height of the added triangle is 20’. We average these two heights to get 17.5’.
Average Height = (15' + 20') ÷ 2 = 17.5'
Next, we multiply the average height by the width of the shape, which is 30’.
Total Area = 17.5’ x 30’ = 525 sq ft
By treating the gable and wall area as a single shape, this approach simplifies the calculation. This formula is applicable whether the shape is symmetrical or asymmetrical, provided a triangle is attached to a rectangle.
Trapezoid
A trapezoid, as shown in the figure below, can be thought of as a rectangle with triangles attached at both ends. The trapezoid has two parallel lengths that differ. To calculate the area of the trapezoid, we find the average of the two parallel lengths and then multiply the average length by either the height or width.
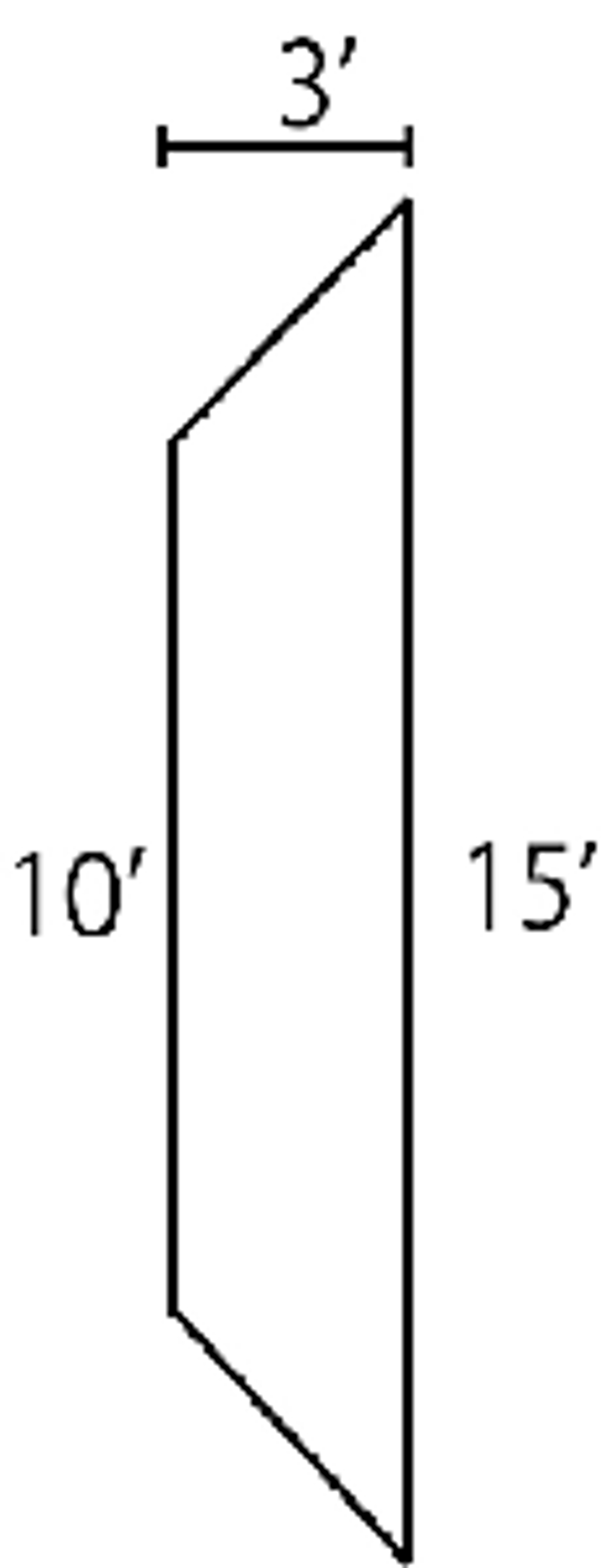
Trapezoid
As depicted in the illustration below, a trapezoid is characterized by two parallel sides of unequal lengths, in this case, 10’ and 15’. To calculate the area of this shape, one must first compute the average length of these two parallel sides.
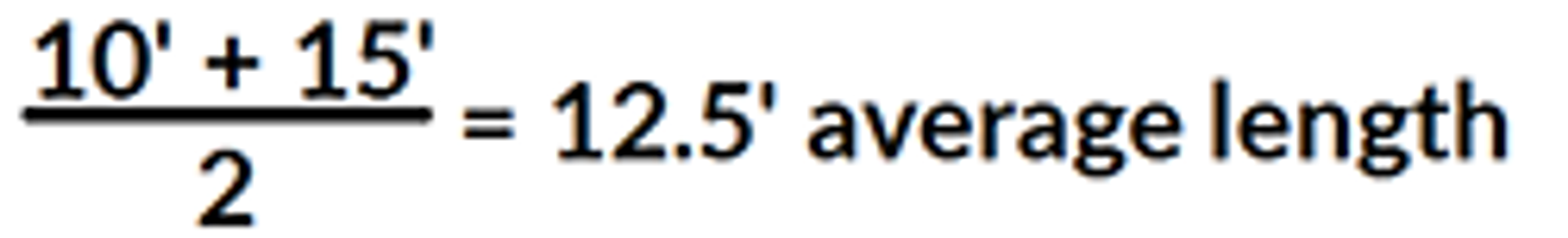
To calculate the area of a trapezoid, take the average of the two parallel lengths and multiply it by the width.
Area = 12.5’ x 3’ = 37.5 square feet.
Hypotenuse
In a right-angled triangle, the hypotenuse is the longest side, represented as side C in the below figure. The Pythagorean Theorem is used to find the length of the hypotenuse, which is:
C^2 = A^2 + B^2
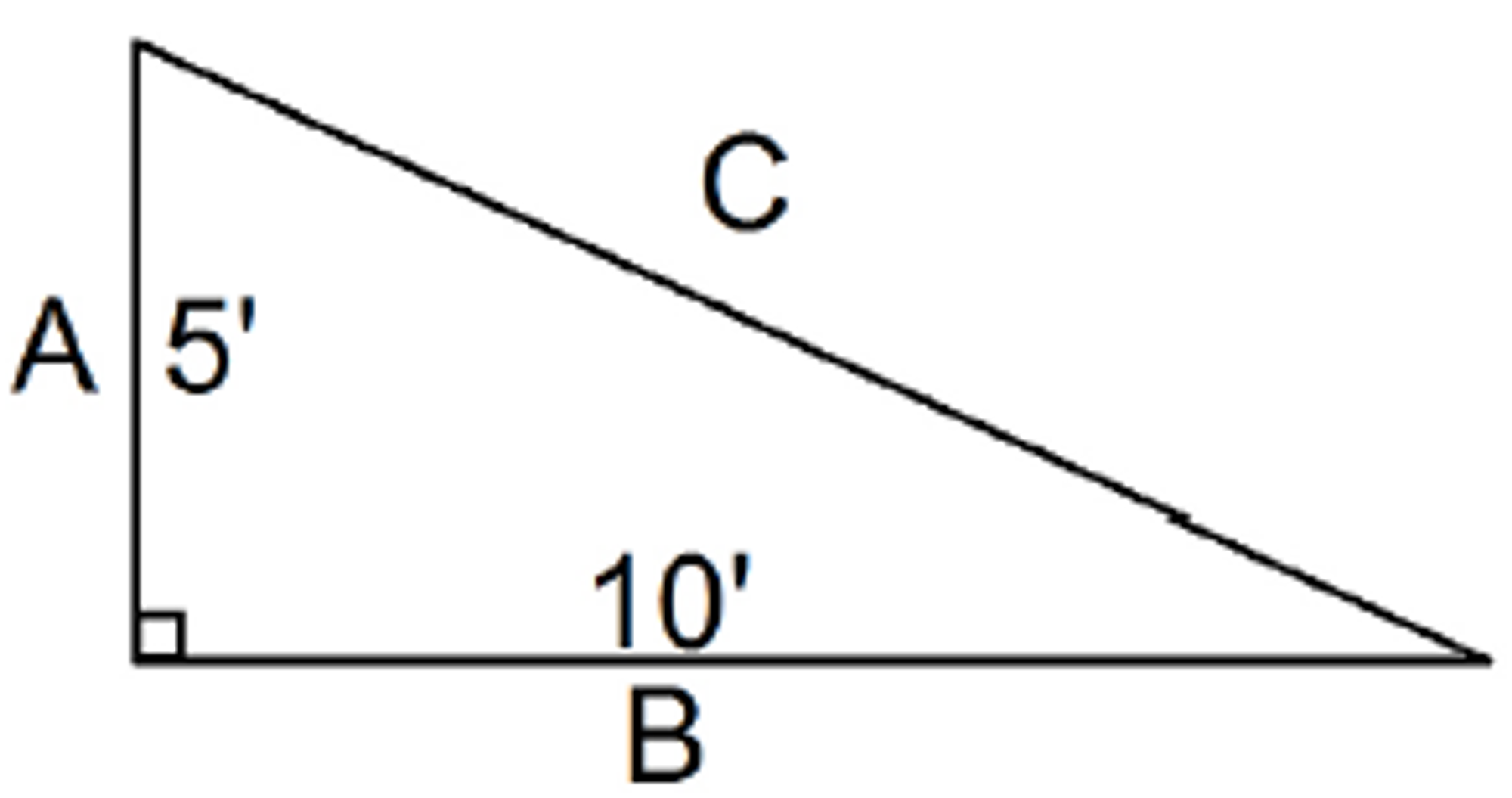
Hypotenuse
Referring to the above image, let's define A as 5’ and B as 10’. By applying the Pythagorean Theorem, we can find the value of C as follows:
Square of A (5²) plus Square of B (10²) equals the square of C (C²)
This gives us 125 as the value for C².
To find C, we take the square root of 125, which equals approximately 11.18’.
Note: Be aware that squaring a number (A²) involves multiplying the number by itself, not by 2.
